解 説
内核の異方性と差動回転が
意味するもの
名古屋大学大学院環境学研究科 吉田茂生
金沢大学理学部地球学科 隅田育郎
1. はじめに
コア・ダイナミクスの研究と地震学の最も重要な接点は,地球の中心にある内核にある.本解説では,内核の成長や外核のダイナミクスと結び付けて,内核の地震学的観測を論じてみたい.より詳細な解説としてはYoshida et al.(1998)や Sumita and Yoshida(2001)を見ていただけると良い.
コア・ダイナミクスを考える上で内核が重要だと考えられるようになったのは,地震学的な異方性の発見(レビューとしてはSong, 1997 ; Creager, 2000 ; Tromp, 2001がある)によるところが大きい.内核が地球全体に占める体積は,1%以下に過ぎない.それだけを考えると,さして重要なところではないように思える.ところが,異方性の発見により,事情は大きく変化した.異方性は,かなりの大きさ(3%程度)で,しかも自転軸に対して軸対称という特異性がある.軸対称ということからすぐに,この異方性が,外核との何らかの関係が原因で作られたことが分かる.それは,内核は固体で粘性が大きいため,内核の流れに直接コリオリ力が効くということが考えられないからである.そのため,内核の異方性の問題は,コア・ダイナミクス全体を解く一つの鍵になっている.
本解説では,異方性の成因論の最近の発展に関してレビューするとともに,異方性に関連して見つかった,内核の差動回転(Song and Richards, 1996)についても解説する.差動回転も,外核のダイナミクスにとって重要な問題である.
2. 内核の異方性の成因
内核の地震学的な異方性がなぜ生じるのかということについては,いまだに議論百出で決着がついていない.異方性の原因としては,一般には,結晶の選択配向(結晶の方向がそろうこと)と,鉄の液体が閉じ込められたいわば流体包有物の形がそろうこととの2種類が考えられる.今のところ,主として前者の議論をする研究者が多い.後者を否定する強い証拠はないが,速度の異方性と減衰の異方性が正の相関を持つこと(Souriau and Romanowicz, 1996)は,流体包有物だとすると考えにくい.また,圧密を考えると,内核が多量に液体を保持しているとも考えにくい(Sumita et al., 1996).そこで,以下では,異方性が結晶の選択配向によるものとして議論する.
異方性が結晶の選択配向によるものだとすると,まず,内核内の鉄の結晶はどういう方向を向いているのであろうか?内核の鉄の安定構造は,最近では量子力学計算によって詳しく調べられてきている.それによれば,内核の鉄はhcp相(e相)である可能性が高い(Stixrude and Cohen, 1995b ; Vocadlo et al., 2000).そうだとすると,弾性定数はc軸を対称軸とするような軸対称性を持っているはずで,c軸方向のP波速度とa軸方向のP波速度のどちらが速いのかが問題になる.弾性定数についても量子力学計算が行われ,基底状態(絶対零度)ではおそらくc軸方向にP波速度が速いと言われてきた(Stixrude and Cohen, 1995a).ところが,ごく最近,有限温度の計算が行われ,従来の基底状態(絶対零度)での知見とは反対に,a軸方向のP波速度が大きいという計算結果が得られている(Steinle-Neumann et al., 2001).それによると,温度が高くなるにつれて,結晶の形がc軸方向に伸びるために,c軸方向のP波速度がa軸方向に比べて遅くなるという.
そのごく最近の計算を信じるとすれば,内核内の鉄はc軸を赤道面に平行に並べるような配向をしているはずだ.そのような配向はどのようにして生じたのであろうか? 従来は,c軸方向にP波速度が速いと思われてきたために,それに合うような成因論が作られていた.そうでないとすると,否定される考えもあれば,そのまま生き残る考え方もある.最新の物性計算の評価はまだきちんとできないので(他のグループの追試が必要),どちら向きのP波速度が大きいかにはこだわらずに成因論をレビューしてみることにする.
結晶の配向は,内核表面で作られるという考え方と,内核内部の流れによって作られるという考え方の2通りがある.表面で作られるという意味は以下の通りである.地球は全体として冷えているから,時間が経つと,固体である内核は,液体である外核から凝固析出してくる.そこで,その析出時に異方性が生成すると考えるのが一つの考え方である(Karato, 1993 ; Bergman, 1997).しかし,外核上部では,異方性が小さい(Song and Hemberger, 1995, 1998)ということを考えると,析出時に異方性が発達するという考えは疑問である.
そうすると,異方性は内核内の流れで生じたということになる.ところが一方で,内核では熱伝導が良いために,内部で熱対流が起りにくい(たとえばYukutake, 1998).だから,流れの原因は別に考えなければならない.これにも大きく2通りあって,一つは内核の異方的成長によるもの(Yoshida et al., 1996)で,もうひとつは電磁気的な力(Karato, 1999)を考えるものである.
内核の異方的成長というのは,次のようなことである.内核は外核から析出してくる.その析出率は外核がどのくらい熱を奪うかに依存している.ところが,外核内の対流はコリオリ力の影響を強く受けており,磁場の効果があまり強くなければ,赤道で熱を最も多く奪い,極で熱の奪いかたが少ないことになる(たとえばOlson et al., 1999).そうすると,内核は赤道でたくさん成長することになる.これが異方的成長である.異方的成長があると,内核は扁平な楕円体になろうとするが,重力があるので,球形に戻る.このことが,内核の中に流れを生じる(図1).このように,内核の異方性は,内核のゆっくりした成長という地球史的な背景があるかもしれない事柄なのである.この考えは,流れの大きさが非常に小さく異方性の発達に時間がかかるのが欠点ではあるが,あとで述べるような長所もあり,すぐに否定できない意味がある.
さて,流れがあるとして,それがどのように結晶を整列させるかにも2通りの考え方がある.ひとつは弾性エネルギーを考えるもの(Yoshida et al., 1996)で,もうひとつは,転位による結晶面のすべり(たとえば,Wenk et al., 2000)を考えるものである.弾性エネルギーを考えるものは,エネルギー自体が小さいという欠点があるものの,次のような著しい長所がある.弾性エネルギーによる選択配向と内核の異方的成長とを組み合わせると,熱流量が赤道と極のどちらで多いかとか,鉄のP波速度がc軸とa軸のどちらの方向に速いかとかいったようなことに依らず,自転軸方向にP波速度が速いという観測と合致する異方性を生じる.これに対して,結晶面のすべりを考えるものは,c軸が流れのシアと垂直方向を向くことが基本になる.その結果が観測されるような異方性を満たすような流れを考えることができれば良い.
以上のように,内核の異方性の成因には,現在はまだ決定版が現れていない.上で説明したように,この問題には,内核の成長という地球史的な問題や,内核における磁場というダイナモ理論に関係した問題などがからんでおり,コア・ダイナミクスのひとつの重要な側面となっている.
最近では,異方性の問題に,さらに複雑な様相が加わってきた.それは,内核表面付近で水平方向の不均質が見つかってきたことである(Tanaka and Hamaguchi, 1997 ; Creager, 1999 ; Niu and Wen, 2001).Creager(1999)の解釈では,内核表面付近の西半球には異方性はあるが,東半球にはないという.一方で,もっと内核表面付近を見ているNiu and Wen(2001)によると,異方性とは関係なく,東半球の方が西半球よりもP波速度が速いという.いずれにせよ,内核の表面付近で,西半球と東半球の違いという東西波数1の不均質が観測されている.
一つの解釈がSumita and Olson(1999)によって外核の流体の室内実験をもとに提案されている.それは,東アジアの下の下降流の集中した地域(いわゆるコールド・プルーム)によって,外核が冷やされ,それが内核における熱流量に波数1の不均質を作るというものである(図2).熱流量に不均質ができれば,前に説明したように内核の成長速度に不均質ができて,それが地震波速度に影響を与えるであろう.このように,内核の問題はマントルまでつながっているのかもしれない.
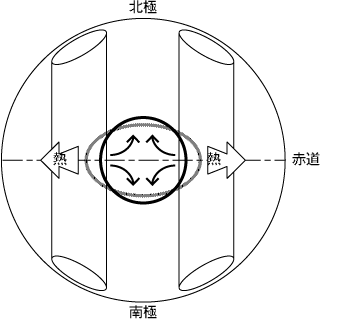
図1 内核の異方的成長により内核内に流れができる(Yoshida et al., 1996)
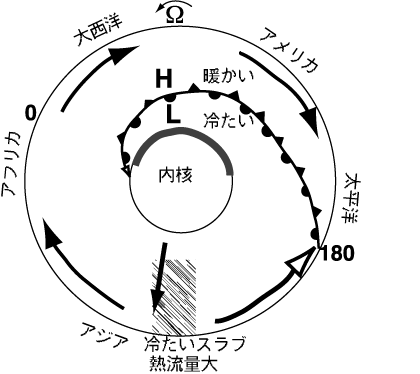
図2 コア・マントル境界の不均質が外核を通して内核にも影響を及ぼす(Sumita and Olson, 1999).コア・マントル境界と内核・外核境界とで,熱流量が大きい部分をそれぞれハッチと太線で示してある.
3. 内核の差動回転問題
本節では,内核の差動回転についてまとめる.内核の差動回転はSong and Richards(1996)によって初めて報告された.差動回転とは,この場合,マントルの自転速度と内核の自転速度とが異なるという意味である.Song and Richards(1996)やSu et al.(1996)といった初期の研究では,1-3deg/yrといった差動回転速度が得られていたが,その後は,この結果に対しては,否定的な研究が出て(たとえば,Laske and Masters, 1999 ; Souriau and Poupinet, 2000 ; Poupinet et al., 2000),差動回転は,あったとしても初期に主張されたほど大きくはないと考えられている(Vidale et al., 2000).差動回転の実際の大きさは,現状ではまだ確定的ではないものの,以下では,差動回転があるかないかの重要性について解説しておく.
差動回転は,内核の異方性の対称軸が自転軸と傾いているというあまり確実とは言えない観測的証拠と,内核を伝播する地震波の速度がある震源と観測点のペアに対して年と共に変化してゆくというこれまたあまり確実とは言えない観測的証拠とに基づいて提唱された(Song and Richards, 1996).その両方が正しければ,これは内核がマントルと異なる自転速度で回っていると解釈できる.結果の信憑性はともかく,そのようにすれば,差動回転を求めることができることを示したことは非常に重要である.
地磁気成因論の立場から言えば,外核の中で,流体の回転角速度の空間変化(これも差動回転と呼ぶ)の分布がどうなっているかを知ることは,非常に重要な意味を持つ.ダイナモ理論の考え方のスタンダードの一つであるいわゆるαωダイナモのω効果(東西方向の流れによって磁力線が曲げられて,東西方向の磁場が増幅する効果)を決めることになるからである.こういう差動回転は,実は地球よりも太陽の方が非常に良くわかっている.それは,地震学的手法(陽震学もしくは日震学)に依っている.そのために,太陽磁場の成因論は大きな衝撃を受けた.非常に粗っぽくいえば,磁場は差動回転の大きなところでたくさん生成される.太陽の観測結果は,対流層の内部では意外にも動径方向の差動回転が小さく,底部に差動回転がかなり集中しているというものだった.そこで,磁場ができているのは,太陽の対流層の底部ではないかという考えが有力になってきた(たとえば,Charbonneau et al., 1999).
残念ながら,地球においては,外核の流れの速さは年間数キロメートル程度で,地震波速度に比べても自転角速度に比べても極端に遅いので,外核内の差動回転を地震学で求めることはほとんどできそうもない.しかし,内核の差動回転が求められるとすれば,それは境界だけではあるけれども,外核の差動回転の情報の一部が得られたことになる.そこで,ダイナモ理論の専門家は,内核の差動回転に注目しているのである.
この差動回転の成因に関しては,この数年の間にすでに紆余曲折があり,混沌としている.Glatzmaier and Roberts(1996)は,数値ダイナモ計算によって,当時の地震学的解析結果と一致する数度/yrの差動回転が産み出されるものとした.しかし,その計算には,過度の(数値)粘性の影響があることが明らかにされたり(Kuang, 1999),マントルによる重力トルクの影響が大きいことが指摘されたりして(Buffett, 1996),最近では,差動回転の大きさは初期の見積もりよりはるかに小さいだろうと考えられるようになっている.最近の数値ダイナモを利用した計算によると,たとえば,0.02deg/yr(Buffett and Glatzmaier, 2000)という値が得られている.差動回転の成因の問題は,理論的には,流体内と流体・固体,固体・固体間の角運動量輸送という問題である.だが,流体内の問題においては非線形がかなり本質的であり,また流体・固体間では,微妙な境界条件の違いが結果に影響してしまう,というやっかいなプロセスである.また,マントル・内核間のトルクも,マントルの密度分布がわからないから,どのくらいの大きさなのかはっきりとはわからない.
Buffett and Glatzmaier(2000)が指摘しているように,差動回転にマントル・内核間の重力トルクが効いているのだとすると,その反作用は地球自転速度の数十年変動の原因でもありうる.従来,自転速度の数十年変動の原因は外核の流れにあると考えられてきたから(たとえばJackson, 1997),内核との重力トルクが原因だということになれば,外核の流れに対するこれまでの研究も大きな影響を受けることになる.
そのようなわけで,内核の差動回転の問題は,外核やマントルの回転の問題と関連しており,大きな関心を持たれているものの,理論・観測とも不確定性が多く,現在は混沌とした状況が続いている.
引用文献
Bergman, M.I. (1997) Measurements of elastic anisotropy due to solidification texuring and the implications for the Earth’s inner core, Nature, 389, 60-63.
Buffett, B.A. (1996) Gravitational oscillations in the length of day, Geophys. Res. Lett., 23, 2279-2282.
Buffett, B.A. and Glatzmaier, G.A. (2000) Gravitational braking of inner-core rotation in geodynamo simulations, Geophys. Res. Lett., 27, 3125-3128.
Charbonneau, P., Christensen-Dalsgaard, J., Henning, R., Larsen, R.M., Schou, J., Thompson, M.J., and Tomczyk, S. (1999) Helioseismic constraints on the structure of the solar tachocline, Astrophys. J., 527, 445-460.
Creager, K.C. (1999) Large-scale variations in inner core anisotropy, J. Geophys. Res., 104, 23127-23139.
Creager, K.C. (2000) Inner core anisotropy and rotation, in Earth’s Deep Interior:Mineral Physics and Tomography From the Atomic to Global Scale, Geophysical Monograph 117, AGU, 89-114.
Glatzmaier, G.A. and Roberts, P.H. (1996) Rotation and magnetism of Earthユs inner core, Science, 274, 1887-
1891.
Jackson, A. (1997) Time-dependency of tangentially geostrophic core surface motions, Phys. Earth Planet. Inter., 103, 293-311.
Karato, S.-I. (1993) Inner core anisotropy due to the magnetic field-induced preferred orientation of iron, Science, 262, 1708-1711.
Karato, S.-I. (1999) Seismic anisotropy of the Earth’s inner core resulting from flow induced by Maxwell stress, Nature, 402, 871-873.
Kuang, W. (1999) Force balances and convective state in the earth’s core, Phys. Earth Planet. Inter., 116, 65-79.
Laske, G. and Masters, G. (1999) Limits on differential rotation of the inner core from an analysis of the Earth’s free oscillations, Nature, 402, 66-69.
Niu, F. and Wen, L. (2001) Hemispherical variations in seismic velocity at the top of the Earth’s inner core, Nature, 410, 1081-1084.
Olson, P., Christensen, U., and Glatzmaier, G.A. (1999) Numerical modeling of the geodynamo: mechanisms of field generation and equilibration, J. Geophys. Res., 104, 10383-10404.
Poupinet, G., Souriau, A., and Coutant, O. (2000) The existence of an inner core super-rotation questioned by teleseismic doublets, Phys. Earth Planet. Inter., 118, 77-88.
Song, X. (1997) Anistoropy of the Earthユs inner core, Rev. Geophys., 35, 297-313.
Song, X. and Helmberger, D.V. (1995) Depth dependence of anisotropy of Earth’s inner core, J. Geophys. Res., 100, 9805-9816.
Song, X. and Helmberger, D.V. (1998) Seismic evidence for an inner core transition zone, Science, 282, 924-927.
Song, X. and Richards, P.G. (1996) Seismological evidence for differential rotation of the Earth’s inner core, Nature, 382, 221-224.
Souriau, A. and Romanowicz, B. (1996) Anisotropy in inner core attenuation : a new type of data to constrain the nature of the solid core, Geophys. Res. Lett., 23, 1-4.
Souriau, A. and Poupinet, G. (2000) Inner core rotation: a test at the worldwide scale, Phys. Earth Planet. Inter., 118, 13-27.
Steinle-Neumann, G., Stixrude, L., Cohen, R.E., and Gulseren, O. (2001) Elasticity of iron at high pressure and temperature - Implications for the Earth’s inner core, Nature, submitted.
Stixrude, L. and Cohen, R.E. (1995a) High-pressure elasticity of iron and anisotropy of Earth’s inner core, Science, 267, 1972-1975.
Stixrude, L. and Cohen, R.E. (1995b) Constraints on the crystalline structure of the inner core-Mechanical instability of bcc iron at high pressure, Geophys. Res. Lett., 22, 125-128.
Su, W.-J., Dziewonski, A.M., and Jeanloz, R. (1996) Planet within a planet : Rotation of the inner core of the Earth, Science, 274, 1883-1887.
Sumita, I. and Olson, P. (1999) A laboratory model for convection in Earthユs core driven by a thermally heterogeneous mantle, Science, 286, 1547-1549.
Sumita, I. and Yoshida, S. (2001) Thermal interactions between the mantle, outer and inner cores and the resulting structural evolution of the core, submitted to AGU monograph Core Dynamics, Structure and Rotation (eds. V. Dehant et al.).
Sumita, I., Yoshida, S., Kumazawa, M., and Hamano, Y. (1996) A model for sedimentary compaction of a viscous medium and its application to inner-core growth, Geophys. J. Int., 124, 502-524.
Tanaka, S. and Hamaguchi, H. (1997) Degree one heterogeneity and hemispherical variation of anisotropy in the inner core from PKP(BC)-PKP(DF) times, J. Geophys. Res., 102, 2925-2938.
Tromp, J. (2001) Inner-core anisotropy and rotation, Ann. Rev. Earth Planet. Sci., 29, 47-69.
Vidale, J.E., Dodge, D.A., and Earle, P.S. (2000) Slow differential rotation of the Earth’s inner core indicated by temporal changes in scattering, Nature, 405, 445-448.
Vocadlo, L., Brodholt, J., Alfe D., Gillan, M.J., and Price, G.D. (2000) Ab initio free energy calculations on the polymorhs of iron at core conditions, Phys. Earth Planet. Inter., 117, 123-137.
Wenk, H.-R., Baumgardner, J.R., Lebenson R.A., and Tome C.N. (2000) A convection model to explain anisotropy of the inner core, J. Geophys. Res., 105, 5663-5677.
Yoshida, S., Sumita, I., and Kumazawa, M. (1996) Growth model of the inner core coupled with outer core dynamics and the resulting elastic anisotropy, J. Geophys. Res., 101, 28085-28103.
Yoshida, S., Sumita, I., and Kumazawa, M. (1998) Models of the anisotropy of the Earth’s inner core, J. Phys. : Condens. Matter, 10, 11215-11226.
Yukutake, T. (1998) Implausibility of convection in the Earth’s inner core, Phys. Earth Planet. Inter., 108, 1-13.