2年生実験
〜誤差と最小二乗法〜
[1] 実験と実験誤差
今回は、実験に必要な最低限の誤差論の話を行う。
世の中、どんなに一生懸命丁寧に測定をしても、ちょっとずれてるみたいだねえ、ということは経験的にはよくある。何度か同じ測定をしてみたときに違った答えが出ると、ますますその感が強くなる。
そこで、真の値と測定値との差を誤差という。といっても、真の値を知りたいために測定をしているわけで、真の値がはじめから分かっているわけではないから、これは仮想的なものである。
(誤差)=(測定値)−(真の値)
ともかく、真の値を測定値から推定したいわけで、そのための努力の仕方は二つある。
(a)誤差をできるだけ減らす…このためには、測定装置を工夫して、誤差要因を減らすように努力する…これは、正攻法で、実験の腕の見せ所
(b)誤差を含んだ測定値からできるだけもっともらしい真の値を求める工夫をする…これが、誤差論・統計学の役割…測定値が多い方が良い値が求められるので「数打ちゃ当たる」作戦、とも言える
それと関連して、誤差には2通りのものがある。何度も同じ測定を繰り返すと、誤差には、「ある値」のまわりにばらつくという性質があるようである。そこで、
(1)系統誤差…その「ある値」と真の値の差…これが小さいのが accurate
(2)偶然誤差…「ある値」のまわりのばらつき…これが小さいのが precise
先程の、努力法(a)は(1)と(2)の両方を減らそうとするものである。一方、努力法(b)は(2)を影響を取り除くための努力である。
[2] 平均値
たとえば、いま、パチンコ玉の直径を3回ノギスで測って 1.11 cm, 1.13 cm, 1.10 cm という数字がでてきたとしよう。数字がばらばらになった理由はいろいろ考えられる。ノギスの使い方が下手だったとか、パチンコ玉が真の球でなかったとか。しかし、とりあえずは、ここではその理由を問わずこれを偶然誤差であると考えよう。
素直に考えると、この場合真の値は平均値に近いであろうと推定する
(真の値の推定値)=(1.11+1.13+1.10)/3=1.11cm
である。このことをどういうふうに数学的な枠組みにのせるか?というのがこれからの説明である。
話を進める前に、ここで、もうひとつの重要な概念である有効数字について確認しておく。今、さきほどの割算の答えを厳密に正しい1.1133333...ではなく、1.11と書いた。なぜか?(中学か高校の復習だと思うのでここには説明を書かない)
話を戻して、平均をもう少し数学的な枠組みに載せてゆく。今まで述べたことを式で書く。
測定値![]() が得られた時、その真の値の推定値は、平均値
が得られた時、その真の値の推定値は、平均値
![]()
と考えるのが良さそうである。
どうしてそうしたいかと思ったかといえば、真の値が![]() だとして、偶然誤差というのは言葉の定義からして、無限回測定をすれば、誤差が正負同じだけあらわれるんじゃないか、つまり式で書くと
だとして、偶然誤差というのは言葉の定義からして、無限回測定をすれば、誤差が正負同じだけあらわれるんじゃないか、つまり式で書くと
![]()
となるんじゃないか、と思うからだろう。測定は有限回だから、真の値の推定値![]() は
は
![]()
とするのが良いだろう。すると、
![]()
ということになり、平均値が真の値の推定値としてもっともらしい、ということになる。
また一方で、ものごとの定式化として、何かを最小にする、という定式化をしたがる人がいる。その場合に上と同じ結果を得るには、
![]()
という関数を考えて、これを最小にするような![]() を求めよ、という問題にすれば良い。これが最小二乗法の一番簡単な場合である。
を求めよ、という問題にすれば良い。これが最小二乗法の一番簡単な場合である。
[3] 母集団と標本
基本的な考え方はこれで良いのだが、しかし、ここでハタと考える。上のような考え方は少し融通が効かない。たとえば、ある測定と別の測定とで、どっちのほうがどの程度信頼できると言うことを知っている時に、真の値の推定値をどう変えたら良いかわからない。また、誤差の出方が必ずしも正負等分にはならないかもしれない。そういういろいろな心配をしだすと、もう少し一般的な枠組みを作っておくと良い。それをやると、上で二乗和を最小にするとした気持ちもわかるようになる。
まず、測定ということを数学的に取り込むための枠組みを説明する。
統計学では、「母集団」というものを考える。これは無限回測定ができたと仮定したときの誤差を含んだデータ全体の集合である。実際の測定は、母集団の中から有限個の「標本」を取り出したものだと考える。
母集団がそういうものだとすると、偶然誤差が正負等分に出るものだとすれば、真の値は、母集団の平均値、すなわち、先に書いたように
![]() (3.1)
(3.1)
を満たすもの、すなわち
![]() (3.2)
(3.2)
であると考えられる。ここまでは、前の説明を母集団と言う言葉で置き換えただけである。ここからが肝心。
データは、0測定ごとに(たぶん偶然に)ばらつくという意味で「確率変数」である。いま、確率変数は1個であるとし、それを![]() であらわす(たとえば、ものさしで長さを測った一回一回の値)。確率変数
であらわす(たとえば、ものさしで長さを測った一回一回の値)。確率変数![]() が
が![]() から
から![]() の間の値を取る確率を
の間の値を取る確率を![]() と書く。関数
と書く。関数![]() を「確率密度関数」と呼ぶ。確率密度関数は母集団を数学的に特定するものである。確率の定義により、
を「確率密度関数」と呼ぶ。確率密度関数は母集団を数学的に特定するものである。確率の定義により、
![]() (3.3)
(3.3)
が成立する。この確率密度関数が誤差の性質に関する情報を持っている。
確率密度関数を用いると先の平均値を表す式(3.1)は
![]() (3.4)
(3.4)
と表現できる。式(3.2)は、(3.3)、(3.4)から導かれる
![]() (3.5)
(3.5)
として表現できる。
この確率密度関数の導入が肝心なところである。ここにわれわれが誤差について持っているすべての情報を入れ込むのである。それによって、誤差の性質が単純でない場合にも柔軟に対応できる。しかし、ここでは一番良く使われる確率密度関数に話を限ろう。それは「正規分布」とよばれるものである。
その正規分布の話に進む前に、母集団を特徴付ける量を2つ定義しておく。それは「母平均」と「母分散」である。母平均は式(3.5)で定義される母集団の平均値である。
![]()
一方、母分散![]() は、確率変数がその平均値のまわりにばらつく度合い(の二乗)を表す量で、
は、確率変数がその平均値のまわりにばらつく度合い(の二乗)を表す量で、
![]() (3.6)
(3.6)
で定義される。
そこで正規分布の登場である。
正規分布
平均![]() 、分散
、分散![]() の正規分布とは、確率密度関数が
の正規分布とは、確率密度関数が
![]() (3.7)
(3.7)
で与えられる分布のことである。この分布を![]() と書く。
と書く。
(問題)式(3.7)が(3.3),(3.5)(もしくは(3.4)),(3.6)を満たすことを確かめよ
こういう正規分布が確率密度関数として一番よく使われる理由は次の定理による。
中心極限定理
母平均が![]() 、母分散が
、母分散が![]() である任意の無限母集団から大きさ
である任意の無限母集団から大きさ![]() の無作為標本を抽出する場合において、その標本平均を
の無作為標本を抽出する場合において、その標本平均を![]() とすると、
とすると、![]() は平均
は平均![]() 、分散
、分散![]() の正規分布にほぼ従う。
の正規分布にほぼ従う。![]() が大きいほど分布が正規分布に近くなる。
が大きいほど分布が正規分布に近くなる。
ここで、標本平均は標本(測定値)の平均値
![]()
である。
この中心極限定理によって、誤差の分布が、正規分布であるという仮定を良くおこなう。中心極限定理は、標本平均に対する定理だから、そうでない確率変数に対しては必ずしも正当化できるわけではないが、誤差というのはいろいろな要因が足しあわされたものだと思えば、無理矢理納得できないわけではない。そこで、確率分布関数に関してあまり他に情報がない時には、誤差が正規分布であるという仮定は良く用いられる。それは、正規分布が指数関数の入った比較的性質の良い関数であるということもあるし、実際問題として測定値の分布が正規分布で近似できる例は多い。
ついでに、この定理からわかる重要なこと(この定理を用いなくても本当はもっと簡単に分かるのだが):データ数![]() が多いと、平均値の推定値
が多いと、平均値の推定値![]() のばらつき(分散)が小さくなる。分散はばらつきの二乗だから、推定値の誤差は
のばらつき(分散)が小さくなる。分散はばらつきの二乗だから、推定値の誤差は![]() となり、データ数の平方根に反比例して小さくなる。
となり、データ数の平方根に反比例して小さくなる。
[4] 正規分布と最尤推定
そこで、このように確率密度関数が正規分布であるというときに、真の値を推定するという問題はどう考えられるだろうか?このような![]() に関して対称的な確率密度関数を使う時には、真の値は母平均
に関して対称的な確率密度関数を使う時には、真の値は母平均![]() であると考えるのが自然である。
であると考えるのが自然である。
問題は「有限の測定値から母平均を推定するにはどうしたら良いか?」ということである。しかし、確率密度関数を導入したことで、問題は「有限の測定値から、確率密度関数に含まれるパラメタ![]() 、
、![]() を求めるにはどうしたら良いか?」と言い換えられることになった。
を求めるにはどうしたら良いか?」と言い換えられることになった。
その問題を次のように考えるのが「最尤推定(さいゆうすいてい;もっとももっともらしい推定)」である。確率密度関数が正規分布の場合に説明する。
母集団![]() から、データ(標本)が
から、データ(標本)が![]() の区間内に得られる確率は
の区間内に得られる確率は
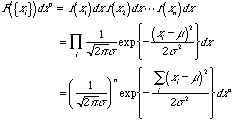 (4.1)
(4.1)
となる。ただし、各測定は独立であるものとした。じっさいに、データ![]() が得られており、母平均を知らないときに、それを推定することを考える。この確率密度
が得られており、母平均を知らないときに、それを推定することを考える。この確率密度![]() を、こんどは母平均
を、こんどは母平均![]() の関数と見て、それを尤度関数と呼び、その尤度関数が最大になるような
の関数と見て、それを尤度関数と呼び、その尤度関数が最大になるような![]() を真の
を真の![]() の一番もっともらしい推定値と考える。
の一番もっともらしい推定値と考える。
尤度関数を最大とする![]() は
は
![]() (4.2)
(4.2)
となり、標本平均と一致する。つまり、標本平均は、母平均の最尤推定値である。
(問題)実際(4.2)のとき(4.1)が最大になることを示せ
同様にして、母分散![]() の最尤推定値を求めると
の最尤推定値を求めると
![]() (4.3)
(4.3)
となる。この
![]() (4.4)
(4.4)
を標本分散と呼ぶ。つまり、標本分散は、母分散の最尤推定値である。
(問題)実際(4.3)のとき(4.1)が最大になることを示せ
(注)実は、標本平均としては
![]()
と定義する方が、本当はふつうである(この意味は各自統計学の教科書を見よ)。また、![]() の平方根
の平方根![]() を「標準偏差(standard deviation, SD)」と呼ぶ。これは誤差の大きさの目安を表す。
を「標準偏差(standard deviation, SD)」と呼ぶ。これは誤差の大きさの目安を表す。
以上のようにして、平均値が真の値の推定値になるという理由付けができた。しかし、これだけでは何のためにこんなに大袈裟な道具立てをしたのかわからないかもしれない。しかし、これで柔軟性が増していることは次の例を考えると分かる。
今、同じ量に関する二つ測定値![]() 、
、![]() があったとする。測定状況の違いなどの理由で測定値
があったとする。測定状況の違いなどの理由で測定値![]() の推定される誤差が
の推定される誤差が![]() 、測定値
、測定値![]() の推定される誤差が
の推定される誤差が![]() であることがわかっていたとしよう。言い換えると、測定値
であることがわかっていたとしよう。言い換えると、測定値![]() の母集団は、平均値が
の母集団は、平均値が![]() 、母分散が
、母分散が![]() 、測定値
、測定値![]() の母集団は、平均値が
の母集団は、平均値が![]() 、母分散が
、母分散が![]() であるとする(
であるとする(![]() 、
、![]() は既知だが、
は既知だが、![]() は未知)。そうした場合の真の値
は未知)。そうした場合の真の値![]() の推定値として何が良いかが、今の論理だとすぐにわかるのである。それは
の推定値として何が良いかが、今の論理だとすぐにわかるのである。それは
![]()
を最小にするような![]() である。
である。
[5] モデリングと最小二乗法
以上のような強力な理論的な道具を得たところで最小二乗法を単に平均値を求めるだけではない使い方で使おう。
ある測定をして、何かの「間接的な量」を求めたいということが良くある。
例:ある場所の重力加速度は、その地下の物質の密度と関係があるから、重力加速度を求めたい。それを、ものが自由落下する様子から決定したいとする。そのためには、ものから手を離してからの時間と、落下距離の組を測定すればよい。
加速度を求めるには、これに2次曲線を当てはめればよい。しかし、実験の誤差があるから、これらの点は正確には一つの2次曲線上にはない。
実験に誤差があることを考えると、これに「一番良くあてはまる」2次曲線を当てはめるのが良いであろう。言い方を変えて整理すると、
(1)結果は2次曲線に乗るはずだという理論(モデル)を信じる
(2)理論と合わない部分は実験誤差であると信じる
(3)そこで結果に「一番良くあてはまるように」2次曲線を描く。
(4)その当てはめた曲線を
![]()
として、![]() を求める。
を求める。
では、「一番良くあてはめる」やり方を先の最尤推定の考え方に則って考えてみよう。仮定として
(1)![]() に実験誤差はなく、
に実験誤差はなく、![]() に実験誤差があるとする。
に実験誤差があるとする。
(2)![]() の実験誤差は、偶然誤差であり、その誤差はどの測定に付いても同じ正規分布をしているとする。
の実験誤差は、偶然誤差であり、その誤差はどの測定に付いても同じ正規分布をしているとする。
を置く。
すると、
![]()
を![]() ,
,![]() について最小化すればよいことがわかるだろう。言い換えると、モデル曲線と実測値
について最小化すればよいことがわかるだろう。言い換えると、モデル曲線と実測値![]() の和の二乗和が最小になるように当てはめるのが良いことが分かる。これを「最小二乗法と呼ぶ」。
の和の二乗和が最小になるように当てはめるのが良いことが分かる。これを「最小二乗法と呼ぶ」。
さて、最小二乗法のやりかたは、一般的に言っても同様。測定値の組![]()
![]() があって、その間にパラメタ
があって、その間にパラメタ![]() を含む関数関係
を含む関数関係![]() があると信じる。
があると信じる。![]() の方に誤差がないとすると、そのパラメタを決めるには
の方に誤差がないとすると、そのパラメタを決めるには
![]()
をそのパラメタ![]() について、最小化する。
について、最小化する。
これを、統計学的にパラフレーズする。データの組![]() がある。測定値
がある。測定値![]() は、母平均
は、母平均![]() 、母分散
、母分散![]() の正規分布をした母集団からの標本であるとする。したがって、この集団に関する尤度関数は
の正規分布をした母集団からの標本であるとする。したがって、この集団に関する尤度関数は
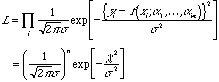
ただし、
![]()
となる。そのパラメタ![]() を決めるには、尤度関数
を決めるには、尤度関数![]() をそのパラメタに付いて最大にする。パラメタは
をそのパラメタに付いて最大にする。パラメタは![]() にしか入っていないので、
にしか入っていないので、![]() をそのパラメタ
をそのパラメタ![]() について、最小化すれば良い。これがとりも直さず、最小二乗法である。
について、最小化すれば良い。これがとりも直さず、最小二乗法である。