第９回　球を過ぎる流れ〜ストークスの流れ〜

６月２３日

本日の内容と重要な式

3-8. 球を過ぎる流れ（Stokes の流れ）

3-8-1. 問題設定：球を過ぎる流れ

3-8-2. Stokes の流れ関数（Stokes's stream function）

、

3-8-3. Stokes 流れの導出

3-8-4. Stokes 抵抗則

3-8-5. 重力場中の運動

3-8-6. 実験：水飴の粘性率を測る

本日のレポート問題（締切：６月２７日昼）

[問題3.3]球が気泡の場合

講義では剛体の球が粘性流体の中を動いてゆくことを考えた。一方で、上の水滴の問題でもそうだが、球も流体でできていることが考えられる。講義とは反対の極端の場合として、気泡のまわりの流れを考えよう。気泡の形は球形のまま崩れないと考える。このとき、流れ関数、抵抗力がそれぞれ次のようになることを示せ。

（ヒント：講義の内容とはでの境界条件が違うだけで、解き方は同じ。今度のでの境界条件は、である。）

講義ノート（3-8-3, 3-8-4）

3-8-3. Stokes 流れの導出

流れ関数を用いて問題を書き直すことを考える。

軸対称な Stokes 近似の式は

である。これに (3.8.9)

、

を代入すると

(3.8.11)

(3.8.12)

となる。(3.8.11)をで微分し、これから(3.8.12)にをかけてで微分したものを引くことによりを消去すると

(3.8.13)

が得られる。これを解けばよい。

境界条件は

、 at (3.8.14)

as (3.8.15)

である。

さて、今の場合はたまたま変数分離型の解がある。変数分離型の解があるとすれば、境界条件から

(3.8.16)

という形の解があるだろうと考えられる。

これを(3.8.13)に代入すると、

(3.8.17)

となる。境界条件は

、 at (3.8.18)

as (3.8.19)

となる。

(3.8.17)の一般解は

の形をしている。

境界条件(3.8.19)より、、

境界条件(3.8.18)より、、

したがって、、

ゆえに流れ関数は

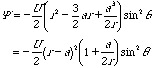(3.8.20)

となる。これで問題が解けた。

速度は流れ関数の定義から、

(3.8.21)

(3.8.22)

となる。圧力は(3.8.20)を(3.8.11)、(3.8.12)に代入して

となることから、

(3.8.23)

と求められる。

3-8-4. Stokes 抵抗則

球にはたらく抵抗を求める。そのためには、球表面に働く応力を求める必要がある。

(3.8.24)

(3.8.25)

この応力の成分を球面全体で積分することで抵抗が得られる。

圧力項からの寄与を圧力抵抗と呼ぶ。

剪断応力からの寄与を摩擦抵抗（あるいは粘性抵抗）と呼ぶ。

両方合わせたものが球にはたらく全抵抗である。

(3.8.26)

これが Stokes の抵抗則である。

実験（3-8-6）

3-8-6. 実験：水飴の粘性率を測る

実験：ストークス抵抗の性質を確かめ、水飴の粘性を求める

Stokes 則による粘性率

水飴：スドージャム（株）製

重量 85 g、体積 61 ml ゆえ、密度は 1.4 g/cm3

Cf. メスシリンダの重量 60 g

スチールボール：

直径　11.1 mm（大）、7.9 mm（中）、4.7 mm（小）

重量　大は1個あたり 5.59 g

したがって、密度は 7.81 g/cm3

講義時間に実験をした結果

落下距離(cm) 落下時間(s) 落下速度(cm/s)

大玉

中玉

小玉

この結果、Stokes 則による粘性は

大玉

中玉

小玉

落下速度がに比例しているか？何となくしているが、あまりしていない。

実は、今の場合、メスシリンダが細いので、壁の影響が大きい。

玉が中心軸上を落下しているとして、壁の補正は以下の補正係数をかけることで行うことができる（「流体力学ハンドブック」p100）。

ただし、（球の径）/（メスシリンダの径）

メスシリンダの径が 29mm であることから、径の比は

大玉

中玉

小玉

となる。そこで、補正ファクターは

大玉

中玉

小玉

となる

補正後の粘性率

大玉

中玉

小玉