基礎セミナー　第９回（７月１７日）

今日の内容：やり残したことの大掃除

1. 前に調べてもらったことで、海流の問題

2. 前回の課題について

3. まとめに代えて Part1：

海の水はなぜしょっぱいかに対するひとつの答え― Kramer(1965) の考え

平衡モデルとストック・フローモデルの関係

4. まとめに代えて Part2：川田さんによる

海水の組成の起源のレビュー

5. Fortran90 に関すること

海の水はなぜしょっぱいかに対するひとつの答え― Kramer(1965) の考え

海の水はなぜしょっぱいかに対して昔々 Kramer(1965) が一つの答えを考えた。

Kramer, J.R. (1965)

History of sea water. Constant temperature-pressure equilibrium

Models compared to liquid inclusion analyses

Geochim. Cosmochim. Acta. 29, 921-945.

答えの骨子：粘土鉱物（教科書3.6.1-3.6.4）などの鉱物との平衡（イオン交換；教科書3.6.6）で海水の組成が決まっている。

　　　　　　ただし、Cl^-は平衡になる相手の鉱物がないので、とりあえず現在の値になる理由を問わない。

その後わかってきたところによると、この答えは正しくない（教科書参照）。しかし、といってまんざら間違いではない内容を含んでいるので、ここで紹介したい。

Kramer はたくさんの種類の化学種を考えていて複雑なので、ここではそれを簡単化したモデルを考えよう。

（Case1）イオンとして、H⁺, Na⁺, Cl^- のみを考える場合

条件１ H⁺と Na⁺とは粘土鉱物を介してイオン交換平衡にある（教科書 3.6.6）

montmorillonite-H + Na⁺ ←→ montmorillonite-Na + H⁺

平衡（教科書 2.3）の式は

　　　　　　　[H⁺]/[Na⁺] = 10^-7.4　　　　　　　　　　　 (1)

条件２ Cl^-濃度は、現在の海水の濃度とする。

　　　　　　　[Cl^-] = 0.55 mol/l (2)

条件３ 電荷の中性条件

[Na⁺] + [H⁺] = [Cl^-] (3)

(1), (2), (3) を解くと

　　　　　　　[Na⁺] = 0.55 mol/l

pH = - log [H⁺] = 7.4

これは、当たり前といえば当たり前の結果である。イオン交換平衡によると、H⁺より Na⁺の方がはるかに多いので、まず、電荷の中性条件から、[Na⁺]は[Cl^-]とほぼ等しくなる。pH は粘土鉱物を介しての平衡から決定される。

とはいえ、当たり前でないこともある。雨の水は空気中に二酸化炭素があるために酸性になる（酸性雨でなくても pH=5.6; 教科書 Box 2.12）。にもかかわらず、海水は少しアルカリ性（pH=7.9）である。これは上のような鉱物との反応で説明できる。実際、水と細かく砕いた石をよくかき混ぜると弱アルカリ性になる。

（Case2）イオンとして、H⁺, Na⁺, Mg²⁺, Cl^-を考える場合

次にもう少し当たり前でなくするために Mg²⁺ も考慮してみる。

条件１ 粘土鉱物とのイオン交換平衡

montmorillonite-H + Na⁺ ←→ montmorillonite-Na + H⁺

chlorite + 10 H⁺ ←→ quartz + kaolinite + 7 H₂O + 5 Mg²⁺

平衡の式は

　　　　　　　[H⁺]/[Na⁺] = 10^-7.4　　　　　　　　　　　 (1)

[Mg²⁺]/[H⁺]² = 10^14.2 (2)

条件２ Cl^-濃度は、現在の海水の濃度とする。

　　　　　　　[Cl^-] = 0.55 mol/l (3)

条件３ 電荷の中性条件

[Na⁺] + 2 [Mg²⁺] + [H⁺] = [Cl^-] (4)

(1)-(4) を解くと

　　　　　　　[Na⁺] = 0.45 mol/l (実際の海水は 0.47 mol/l）

[Mg²⁺] = 0.05 mol/l (実際の海水は 0.054 mol/l)

pH = - log [H⁺] = 7.7 (実際の海水は 7.89)

が得られる。

これは Case1 よりも海水の値に近づいている。粘土鉱物との平衡の平衡定数がちょうどうまい具合になっているからだ。

こんなことをもっと詳しくやって Kramer は、上の考えが結構うまくいくことを示して、このような平衡で海水の組成が決まっているのではないかと考えた。ところが、実際の深海堆積物を調べてみると、そんなに平衡が成り立っていないみたいなのでおかしいということになってきた。その後、Mg については海底熱水循環が大きな役割を果たしていることがわかってきた（教科書 表4.2, Box 4.7, p.178）。Na については、粘土鉱物の役割は本当はどの程度なのか確かなデータはないが、そう大きくはないだろう（教科書 p.181）。とはいえ、考え方としては重要なのでここで紹介した。

平衡モデルとストック・フローモデルとの関係

上で紹介した平衡モデルと拡張すると、先週のストック・フローモデルに組み込むこともできる。上のCase1の場合にそれを行うと以下のようになる。ただし、正直にこの計算を実行すると海水がものすごい酸性になったりすることもありうるので、あまり現実的ではないかもしれない。

イオンとして、H⁺, Na⁺, Cl^- のみを考える。

仮定１　[Na⁺]は、時定数（滞留時間）τで平衡に近づく

仮定２　[Cl^-]は一定

仮定３　常に電荷の中性条件は満たされる。

上の仮定の下で、[Na⁺]の時間変化を考えてみる。まず、先週やったことから、おおざっぱには

となるだろうと考えてみる。ここで、は海の体積、は平衡濃度である。ここで、平衡条件と電荷中性条件から

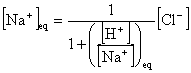
と書ける。

時間がたつと、濃度はやがて定常状態になる。大切なことは、そのときの濃度は平衡濃度ではなく

となるということである。平衡に達するまでにある程度時間がかかって、その間にも次々に流入があるので、定常状態の濃度は平衡濃度よりも大きくなる。だから、Kramer の議論は平衡に達するまでの時間τが短いときにのみ成立し、平衡の計算で数字がたまたま現実の海水に近いとしても、すぐに「だから正しいのだ」と安心することはできないことがわかる。