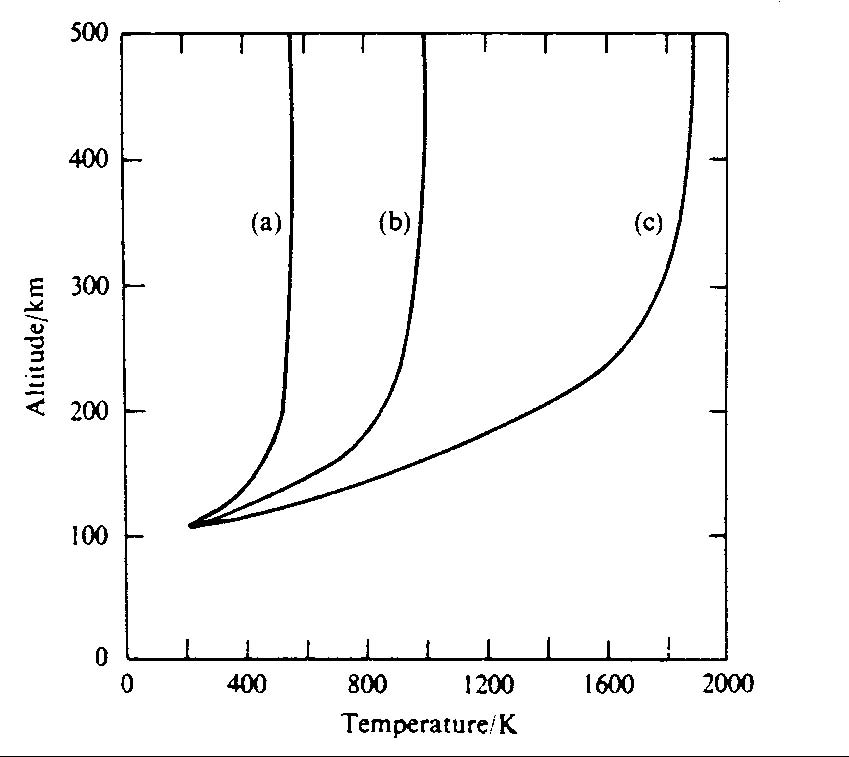
温度構造は太陽活動度によって異なる。それぞれ太陽活動度が a) 非常に弱い、b) 並、c) 非常に強い、状態に対応する [ 直接的には GFD-DENNOU : genshou.earth.html による。 その元は Houghton (1986) で、その原図は COSPER (1972) ]
(星の寿命)×(エネルギー放出率)=(核融合で生成しうるエネルギー)
太陽の寿命を考えてみよう。
(太陽の寿命)= 5 x 1017 s = 1010 yr = 100 億年
次に、質量による寿命の違いを説明する。
L 〜 σT4 R2 / (κρ R) 〜 σT4 R / (κρ) 〜 σT4 R4 / (κ M)主系列星では、熱エネルギーと重力エネルギーが釣り合っているが、 温度 T は水素の燃焼温度で決まっているので、熱エネルギーが決まっていて、 重力エネルギーは質量に依らないことになる。そこで M ∝ R。 したがって、もし κ が一定ならば、L ∝ M3。
しかし、長い時間経てば、この割合が変化する。ある人の計算によると (出典:日経サイエンス 2008 年 6 月号 L.M. Krauss and R.J. Scherrer 「宇宙の歴史が消える日」(pp.22-29) の中で引用されている Fred Adams と Gregory Laghlin の計算結果)、
| 水素 | ヘリウム | He より重い元素 | |
|---|---|---|---|
| ビッグバン(から数分後) | 76 % | 24 % | 0 % |
| 現在 | 70 % | 28 % | 2 % |
| 1兆年後 | 20 % | 60 % | 20 % |
と予想されるのだそうである(数字は質量比であり、原子数比ではないことに注意)。 現在は、ビッグバンの時からそれほど変っていない。 しかし、変っていないとはいえ、He より重い元素が 2 % できているということは 重要である。He より重い元素があるからこそ、地球のような惑星やわれわれの ような生命が生まれることができるのである。1兆年も経つと、元素組成の 観点からは、ビッグバンの痕跡が消えてしまう。
He より重い元素の量の個別の進化も計算されているようである。 野本編 (2007) 「元素はいかにつくられたか」(岩波書店)では、 Kobayashi et al. (2006) Galactic Chemical Evolution: Carbon Through Zinc The Astrophysical Journal, 653, 1145-1171. という論文の結果が引用されている。
一方、恐竜を絶滅させた隕石は、直径 10 km 程度と考えられている。 それは、その隕石が作ったと考えられる Chicxulub クレーターの直径が 200 km 程度で、その 1/20 程度というのがクレーター形成のモデルで 通常考えられている衝突天体の大きさだからである。
参考文献:熊澤・伊藤・吉田編 (2002)「全地球史解読」(東大出版会) 6.6.2 節(海保邦夫著)
| 熱圏 (thermosphere) | 80 - 500 km | |
| 外圏 (exosphere) | 500 - 10,000 km | 分子どうしの衝突がない |
まず、熱圏の温度は、以下の図のように太陽活動度によって大きく変わる。

温度構造は太陽活動度によって異なる。それぞれ太陽活動度が
a) 非常に弱い、b) 並、c) 非常に強い、状態に対応する [
直接的には GFD-DENNOU : genshou.earth.html による。
その元は Houghton (1986) で、その原図は COSPER (1972) ]
次に、外圏になると、大気が希薄で分子どうしが衝突しないので 普通の意味での温度が定義できない。
「地球が赤外線を放出して冷える」のは「まわりが透明(真空)だから」である。 ふつう、「冷えるのはまわりの温度が低いから」ということが多いのだが、 それは「温度」がきちんと定義できるときに限る。
光に対して「温度」が定義できるのは、十分に不透明な場合に限られる
(詳細を略する)。赤外線に対しては、対流圏はけっこう不透明なのだが、
それより外は透明である(自由に光が出てゆく)。対流圏くらいだと、
光(赤外線)によって温度が低い方にエネルギーが運ばれると言って良いが、
そこから外は、光はだいたい自由に出て行っている。それで、冷える。
3 K の話は置いておいて、とりあえず背景輻射の説明をしておく。
宇宙のどの方向からも同じような光(マイクロ波)がやってくる。
これを背景輻射と呼ぶ。この広い宇宙のどっちの方向からも
同じような光が来るのはとっても不思議である。しかし、ビッグバンがあって、
宇宙(の少なくともわれわれに見えている範囲)はかつてはとても近かった
と考えれば、不思議さが解消する(正確にはこれはインフレーションモデルの話)。
たとえて言えば、双子は同じ親から生まれたはずだ、ということである。
他人の空似は考えにくい。
では次に 3 K がどういう意味で温度かを説明する。次のように、
太陽の光のアナロジーで考えると良い。
太陽から来る光は 6000 K であるということができる。
太陽の表面(不透明と透明の境界)では光の温度がきちんと定義できて
6000 K で、あとほとんど透明な部分を通過してくるから変わらないと
いう意味で 6000 K である。しかし、熱くはない。それは、広がって
薄められているからである(熱平衡ではない)。でも、虫眼鏡で集めると、
最高で 6000 K までは上げることができる(証明は難しいので省略)。
光を1点に集中させると 6000 K よりも高くできそうだが、実は太陽からの光は
厳密には平行光線ではないので、光を1点には集中させられない。それで、
6000 K 以上まで上げることはできない(杉本大一郎「いまさらエントロピー」)。
宇宙の 3 K もだいたいそんなような意味で温度である。まとめると、物質の温度は、
原子や分子の相互作用が十分に行われているときにのみ定義ができる。
光の温度は光と物質の相互作用が十分に行われているときにのみ定義ができる。
それ以外でも温度が定義できる場合があるが、どういう意味で温度なのかは
常に注意しておく必要がある。温度なんてみんなわかっているつもりでいる
かもしれないけど、普通でない状態でどう定義するかは常に注意しておく必要がある。
しかし、実は、この言い方には不親切な点がある。まず、外核は P 波しか通らないのに、
なぜ内核に S 波が通るのかという疑問が起こるかもしれない。P 波が内核の表面に垂直に当たると
確かに内核には P 波しか行かないのだが、斜めに当たることを考えると、P 波の一部が
S 波へ変換されることがわかる。そこで、P 波(外核)→S 波(内核)→P 波(外核)という
変換が起こることがあり得て、それを観測すれば、内核が固体であることが分かる。
ところが、実はこの変換効率などをきちんと考えると、この波は検出限界ぎりぎりである
ことがわかる。実際、観測されたという報告もあるが、なかなか際どい。
しかし、波長と周期の長い波(地球全体が揺れるようなもので、P 波と S 波が渾然一体となる。
自由振動と呼ばれる)を使うと、内核が固体であることが分かる。
歴史的には、こちらの方で内核が固体であることがわかった。
ものが惑星を飛び出すことができる速度は脱出速度と呼ばれており、
運動エネルギーが重力エネルギーに打ち克つというところから
問 3-3-2「上の問 3-3-1 の答えでは真空の宇宙空間では温度が定義できないと
している。しかし、3 K 背景輻射というものがあると聞いた。
これは矛盾ではないのか?」
この講義では以前には触れなかったが、ビッグバンの証拠として 3 K 背景輻射と
いうものがある。宇宙空間で温度が定義できないと言ったこととこれは矛盾しない。
3 K は狭い意味では温度ではない。もはや宇宙は透明で
光と物質は相互作用しないので、熱平衡の意味での温度は定義不能なのである。
3-1 固体地球の形成、組成、構造
問 3-4-1「外核が液体で内核が固体だとどうして地震学からわかるのか?」
地震波には P 波(縦波)と S 波(横波)とがある。P 波は液体中も固体中も通過できるが、
S 波は液体中は通過できない。この性質を使うと、液体と固体を区別できる。
3-4 地球以外の惑星たち
問 3-4-1「講義では水星には大気がないということだった。惑星が大気を
持てる条件は何か?」
[step1] まず、惑星が大気を持つことができる最低条件として、
大気の熱運動が重力に打ち克って大気が逃げて行くことがないという
ことを考えてみよう。これを式で表してみる。
1/2 vesc2 = G Mplanet / Rplanet
で表すことができる。一方、空気分子の熱運動の速度の各成分の大きさは、
だいたい
1/2 m vth2 = 1/2 R T
と表すことができる。もちろんすべての分子がこの速度で動いている
わけではないが、だいたいの平均値がこのように表される。
これらの量を地球型惑星で求めてみよう。
| Mplanet | Rplanet | S(太陽定数) | T | vesc | vth | |
| 水星 | 3.14×1023 kg | 2.44×106 m | 9.14×103 Wm-2 | 448 K | 4.14×103 m/s | 2.91×102 m/s |
| 金星 | 4.87×1024 kg | 6.05×106 m | 2.62×103 Wm-2 | 328 K | 1.04×104 m/s | 2.49×102 m/s |
| 地球 | 5.97×1024 kg | 6.38×106 m | 1.37×103 Wm-2 | 279 K | 1.12×104 m/s | 2.29×102 m/s |
| 火星 | 6.42×1023 kg | 3.40×106 m | 5.90×102 Wm-2 | 226 K | 5.02×103 m/s | 2.07×102 m/s |
以上の計算からは、すべての地球型惑星は二酸化炭素程度の分子量の 大気を持つことができるという結論が得られる。ただし、この中での 傾向としては、水星大気が最も散逸しやすいことがわかる。
[step2] にもかかわらず、水星に大気がないのはなぜか?
実際は、大気が光や太陽風などとの相互作用で加速されて逃げて行くという 非熱的散逸が重要である。しかし、この過程はケースバイケースなので、 なかなか定量的に議論するのは難しい(水星についてはある程度議論されている)。 現在の太陽系を見ると、現在の水星には大気がなく、 火星からは大気がかなり失われた痕跡がある。このことから、結果論的に言えば、 火星サイズ以下の天体だと、太陽系年齢程度経てば非熱的散逸により 大気が失われると考えられる。[この段落の内容は、阿部豊氏私信による]
まず、マントルと外核が大きく異なる速さで回っていたとすると、その影響は磁場である程度 わかるはずである。外核の自転速度といっても、深さによる変化もあるからそう簡単ではないが、 以下の2つのことが言える。
次に内核の方はもし大きく違う速さで回っていると地震学的に観測可能である。 地震学によると、マントルとの自転角速度差はあったとしても1年に1°以下と推定されている。
そういうわけで、今のところは、コアとマントルとの自転の角速度差は、外核にせよ内核にせよ、 たかだか1年に1°で、たぶんそれよりだいぶん小さいと考えられている。
この問題はダイナモ問題にとってもきわめて重要である。 地球でも太陽でも、内部の対流で磁場ができている。磁場を作る重要な要因のうちの ひとつに、磁場生成部分の自転速度が場所によってどうちがうかということ (差動回転という)がある。 言い方を変えると、東西流の分布だ。この観測は、驚くべきことに 地球よりも太陽の方が進んでいる。太陽でも地震学のような手法で 内部の観測ができる(日震学、陽震学)。それを使うと、太陽では 差動回転が大きいために、自転速度分布がわかってしまう。地球では、 まだよくわかっていない。
あと、関連する問題として、木村栄(ひさし)による z 項の発見がある。 木村栄は第1回文化勲章受章者のひとりである。地球の自転軸は、 時々刻々ほんの少しだけ動いていることが知られている。 これが歳差、章動、極運動という名前が付いている現象だ。 詳しいことは省く。1890 年くらいから、この自転軸の運動の国際的な 観測プロジェクトが始まった。その日本の責任者が木村栄だった。 観測を始めてみると、日本のデータが理窟に一番合わずに、ヨーロッパから 非難された。けれどもよくよく調べてみると、昔の理窟の方がおかしいということを 木村は発見した。その部分を z 項と言う。これは、明治時代、 科学の後発国であった日本の実力が世界レベルになったことを示したものだった。 それで、木村は文化勲章をもらった。それと今の話の関係だが、 z 項の原因は木村が生きている間はわかっていなかった。 結局わかったことは、マントルと外核の自転のしかたのちょっとしたずれが 原因であるということだ(専門用語では「流体核共鳴」の効果。詳しくは 日置幸介氏による解説を見よ)。
そこで、現在のような深層循環になっている理由を説明しようとすると、 どうしても結果論的になるのは、しかたがない。 結果的には、北太平洋と北大西洋では塩分が大きく異なる。 北太平洋の塩分は 33 パーミル程度。これに対して、北大西洋の塩分は 34-35 パーミルくらいである。このわずかな違いが問題である。そうすると、温度が 同じでも密度が 1 パーミルくらい違うことになる。こういうわずかな差が 海洋の循環にとって重要だというのが、海洋循環の微妙な点である。
ではその違いがどうして生まれるのかといえば、ひとつの大きな理由は、 北大西洋では北太平洋よりも蒸発量が比較的大きいために、塩が濃縮される せいである。なぜ蒸発が大きいかと言えば、深層循環とメキシコ湾流が 合わさって暖かい水を北大西洋に運んでいるために、水温が高いからである。 一方、北太平洋では深層の冷たい水が上昇してくるので水温が上がらず、 蒸発量が小さい。つまり、現在のような海洋の循環があるために、蒸発量の 差が生まれて、現在のような海洋の循環ができている。論理が循環している ようだが、多重解があるような系では、説明は必然的に結果論的になる。
温度が高い方が沈みやすいというのもパラドキシカルな話だが、 0度付近では密度の温度依存性は小さいので、塩分が重要になっている。
参考書:The Open University, "Ocean Circulation, 2nd ed." (2001)
とくに 6.6 節
塩分の図:Texas A&M 大学 海洋学テキスト 6-3 節 Fig.6.4