Generalized Spherical Harmonics (GSH) 入門

0. 口上

本日の話はオリジナルなものはなくて、「一般化された球面調和関数」という特殊技術の解説である。数年前にこれを使った研究をしていて、さてまとめようと思ったらだいぶん忘れていたので復習をした。その結果の発表である。

1. 問題の発端―関数展開と対称性

数値計算やあるいは解析的に問題を解こうと思うとき、ある種の関数で変数を展開してから解くということをよくやる。

たとえば、Fourier 変換は、三角関数（指数関数）で展開する

また、有限体積法や有限要素法では、ローカルな関数で変数を展開する。

で、どういう関数で変数を展開するのが良いか？ということを考える一つの指針が対称性から自然に導かれる関数を用いる、ということである。

結論を言っておけば

並進対称性のある問題では、指数関数を使うのが良く（Fourier 変換）、

球対称性のある問題では、球面調和関数を使うのが良い。

以下では、主として球対称性を考える。

まず、対称性を用いるという気持ちを解説することから始める。

1-1. 関数展開と固有関数

考える問題は次のようなものである。

ここで、は、空間に関する線形演算子であるとする。

さて、このを何かの関数で展開することを考える。一番望ましいのは演算子の固有関数で展開することである。もし固有関数がわかっていて

なんていうふうになっていれば、問題は簡単。

のように初期条件を展開しておけば

が答えで、問題がいっぺんで解けてしまう。

しかし、演算子の固有関数を求めるなどというのは、問題を解くというのにほとんど等しいようなもので、そもそもその問題を解くのにどういう関数で展開したいかということが問題である。ここで紹介する方法では、問題の対称性を使うと、固有関数のうちのその対称性に関わる部分が問題を解く前からわかってしまうというのが肝要な点になる。

1-2. 回転対称性の数学的表現

演算子が球対称であるとする。球対称であるという意味は、系を回転しても（座標系の方を回しても良い）、演算子の形が変わらないという意味である。具体的にはどうすれば良いかというと、系を回転する行列をとして

(1.2.1)

などといった変数変換をして演算子を書き換えた時にまるで形が変わってなければ良い。

演算子が回転操作の後での表現を求めるために、まず、関数に対する回転操作を定義する。座標が (1.2.1) のように変換されると、回転後の関数は

(1.2.2)

で表される。すなわち、関数に対する回転演算子は

(1.2.3)

すなわち

(1.2.4)

で定義される。

さて、それで演算子の回転後の姿を考える。先に関数を回転しておいて、回転後の演算子を演算したものは、先に演算子を演算してから回転したものに等しいはずである

(1.2.5)

すなわち

(1.2.6)

or

(1.2.7)

である。

演算子が回転対称であるとは

(1.2.8)

ということだから

(1.2.9)

すなわち、が回転演算子と可換であることにほかならない。

1-3. 対称性と固有関数

線形代数の重要な定理

可換な演算子は共通の固有ベクトル（固有関数）を持つ

（略式の証明）

可換な演算子をとする。

まず、の固有値、固有関数が

となるものとしよう。簡単のため縮退（同一固有値の固有関数が複数

あること）はないものとしよう。

さて、いまの固有関数のひとつを取ってきてという量を考えると

となるから、は固有値に属するの固有関数である。の固有関数に

縮退はないとしているからこれはの定数倍でないといけない。ゆえに、

すなわち、はの固有関数でもある。

この定理によって、演算子の固有関数を直接求める代わりに、回転演算子の固有関数（のようなもの）をきちんと調べておくと、演算子の固有関数のうち少なくとも回転対称性に関わる部分の面倒は見てくれるはずだ、ということがわかる。

いきなり回転はむずかしいから、まず簡単な並進対称な場合を考える。関数を軸方向にだけ平行移動するという演算子をと書くと

(1.3.1)

である。固有関数は

であることが容易に分かる。というのも

(1.3.2)

だからである。だからこそ Fourier 変換は、並進対称性のある系において非常に便利なのである。

2. 既約表現とその基底

2-1. 固有値の概念の拡張としてのの既約表現

ところで、一方で、実は、回転対称性の場合には、並進対称の場合にはない別の問題がでてくる。それが先に固有関数のようなものと書いた理由である。それは、軸のまわりと軸のまわりの回転が可換でないというように、回転操作どうしが可換でないために、すべての回転演算に対する固有関数というものが存在しないからである。そこでちょっと条件を緩める。すべての回転演算に対して定数倍を除いて不変な関数を求めるのではなく、すべての回転演算に対して定数行列倍を除いて不変な関数の組を求めるということにする。群論の言葉では、そのような行列を回転群の既約表現と言い、そのような関数の組を既約表現の基底という。ここで、回転群というのは回転操作全体の集合のことである。すなわち、既約表現は固有値を拡張したもの、既約表現の基底は固有関数を拡張したものである。

式で書くと、既約表現の基底を

として

と書けるということである。ここで、が既約表現である。添字の範囲は有限である。

先程の定理の拡張は次のようになる。

回転対称な演算子の固有関数は、回転群の既約表現の基底で表現できる

（回転群の既約表現に属する）

（略式な証明）

演算子の固有値、固有関数を

とする。この際は縮退を許し、一つの固有値に固有関数の組が

対応するものとしよう。

さて、いまの固有関数のひとつを取ってきてという量を考えると

となるから、は固有値に属するの固有関数である。固有値に

属するの固有関数はの線形結合で書けなければならないから

すなわち、演算子の固有関数は回転群の何かの既約表現に属する。

回転操作の場合、結論を先に述べると、そのような既約表現およびその基底（のひとつの選び方）が実は GSHで、基底に球面上のスカラー関数という制約を加えたものが通常の球面調和関数となる。

2-2. 既約表現の定義の抽象化

ここで、後の便宜上、既約表現の定義をもう少し抽象化する。

回転操作とを続けて行うという回転操作をとする。すなわち、

で、これに対応する回転行列を

とする。そのとき、

であり、一方で

であるから、

という性質があることがわかる。

そこで、定義をひっくり返す。回転行列の関数となっている行列があって

ならば

という性質をもっている時（準同型写像）、を回転群の表現という。最も単純な表現は、すべてのに対してとしてしまうもので、これを恒等表現という。また、回転行列自身は表現の一種である（）。

表現のうちで、いかなる線形変換によっても、すべての回転行列に対して

という形にできない「極小の」表現を既約表現という。

こうやって、定義を抽象化してしまうと、表現が表現の基底から独立してしまうので、基底をかならずしも考えなくても表現を考えることができる。それと同時に、ここで重要なことは、基底を空間の関数に限らなくて良くて、基底にいろいろの種類のものを考えることができる。後で見るように、GSH の話では、回転操作の関数を基底に取るという考え方が有効に使われる。

3. 回転群の既約表現

3-1. 回転の表し方―オイラー角

話を具体的に進めるために、一般の回転の表し方を考える。その代表がオイラー角である（下図）。

オイラー角によれば、任意の回転が以下の３つのステップで表される。

(1) 軸のまわりの角度の回転。これによって、座標軸はからに移る。

(2) 軸のまわりの角度の回転。これによって、座標軸はに移る。

(3) 軸のまわりの角度の回転。これによって、座標軸はに移る。

まとめると

と表現できる。ここで、あとから大切になる点は、北極が移動した先が、極座標でで表される点に移っていることである。このことから、回転と空間座標を対応させることができる。すなわち、空間座標の点はと表すことができる。このことをあとで用いる。

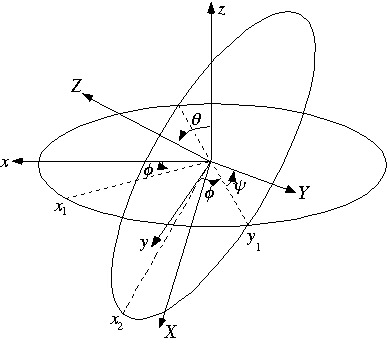
その対応付けと関連して、北極にあった軸方向の単位ベクトルがどのように移動されるかも見ておくことが重要である（下図）。

この図から、オイラー角がのとき、北極にあった直交単位ベクトルは極座標の基底単位ベクトルに移り、オイラー角がのとき

に移ることがわかる。このことも後で用いる。

◎ ここから回転の表し方を便宜上ひっくり返す

以上のような回転の表し方はふつうだが、後の便宜を考えると、符号をまったくひっくり返して定義しておくのが良い。すなわち、という角度で特徴付けられる回転によって、極座標で表される点が北極に移り、基底ベクトルが北極での基底ベクトルに移るとするものである。そうすると、空間座標の点はと表されることになる。

なお、オイラー角の逆向き回転に対応するオイラー角はである。

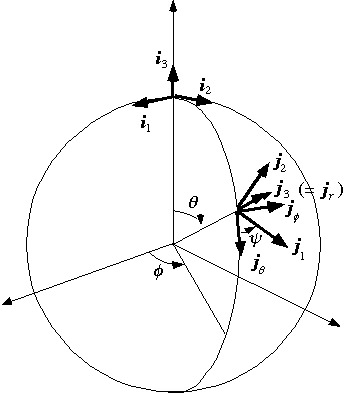
3-2. 回転群の既約表現

回転群の既約表現をオイラー角の関数として具体的に求めることができる。そのやりかたは数学的テクニックをいろいろと駆使するのだが、今日は途中を省略して結果だけを書いておく。

回転群の既約表現は、自然数で特徴付けられる。既約表現は次の正方行列であって、その要素は

である。ここで、は Jacobi 多項式と呼ばれる関数で、Legendre 陪関数の親戚である。詳細な説明は省くが、ここでというような量が出てくる理由は、だけ平行移動する操作の表現がとなることからのアナロジーで理解できるだろう。指数関数の肩の符号が違うのは、さっき回転の表し方をひっくり返したせいである。また、とくには恒等表現である。

3-3. 回転操作の関数に対する回転操作の定義と、そのときの表現の基底

既約表現が表現であることを用いると、既約表現自身をひとつの基底とするような表現をただちに構成することができる。それは回転群の上における表現である。

まず、既約表現が表現である以上は

(3.3.1)

のとき

が成立する。一方で、表現と基底の関係は

(3.3.2)

というものであった。これらを見比べてやると、回転操作の関数の回転を次のように定義してやるとよい。それは、

(3.3.3)

とすることである。このとき、が既約表現の基底となっていることが

(3.3.4)

からわかる。

4. 球面調和関数と一般化された球面調和関数

ここで初期の目標に到達する：球面上の関数（スカラー、ベクトル、テンソル）の空間の上で、既約表現の基底を見出すこと。

4-1. 球面調和関数

まず、3-1. で説明したように、ここでの定義だと、オイラー角の回転によって、極座標でで表される点が北極に移る。そこで、空間座標の点はと表される。すると、1-2 で述べたことから、球面上のスカラー関数に対する回転操作は (1.2.4) 式のように

(4.1.1)

と書ける。

一方、この関数は回転群上の関数とみなすこともできて、(4.1.1)は

と書けるからちょうど(3.3.3)の変換則を満たしていることがわかる。実は、こうしたいがために、3-1. では回転の符号をひっくり返しておいたのである。

したがって、を展開するのに相応しい関数は、すなわち

ということになる。いまの場合、は余分な変数なので、だけ取れば良い。こうして得られた

が球面調和関数である。ただし、ここでとの記号を入れ替えた。

4-2. ベクトル関数の展開と一般化された球面調和関数

ベクトル関数の展開は、成分ごとに球面調和関数をすれば良いかというと、そうはいかない。なぜなら、成分ごとに回転変換則

が満たされているわけではないからである。

ところが、3-1 ででてきた基底ベクトル は回転と一緒に回るので、この基底に関する成分は

のように回転してくれるはずである。

(4.2.1)

であったから、

(4.2.2)

である。

これをもう少し形式的に書くと以下のようになる。いまベクトルのデカルト座標、すなわち、北極での基底ベクトルに関する成分をと書く。そして、 に関する成分をと書くことにする。回転で基底を回すと基底になるというように回転を定義したので、

の関係がある。このことから、煩雑だが単純な計算により

(4.2.3)

が得られる。一方、ベクトル場を回転させると、

(4.2.4)

だから、

(4.2.5)

となって、期待通りの変換則を満たす。(4.2.5) は、(4.1.1) と同じ形をしており、は、回転に伴ってスカラー関数のように変換される。そこで、は「スカラー成分」と呼ばれる。

このスカラー成分のそれぞれを球面調和関数展開すれば良さそうだが、もう一押し必要。今や、(4.2.3) から見て取れるように、はの関数だから、依存性の面倒を見ておかないといけない。回転群の既約表現の形と(4.2.2)とを比較すると、

という量を使うのが便利そうである。

以下、前と同様に、関数やを展開するのに相応しい関数は

ということになる。依存性に着目すると、はの関数を使うと良く、はを使うと良い。はスカラーのときと同じくを用いる。最後に共通因子ので割ってしまうと、

で、を展開すれば良いということになる。これが、ベクトルを展開するのに用いる一般化された球面調和関数である。

以下同様にして、高階のテンソルの展開にはの大きなものを用いれば良い。このようにして、回転群の既約表現を利用して一般化された球面調和関数を構成できる。

5. 最後に

このような展開で便利なのは、微分したり積分したり、積を取ったりする時に、群の表現論から得られる性質を利用できることなのだが、それは今回は時間がないからできない。御希望なら大学院講義にしても良い。

参考文献

Gel'fand, I.M. and Shapiro, Z. Ya (1956) Representations of the Group of Rotations of 3-Dimensional Space and their Applications. American Mathematical Society Translations, Ser2 Vol2 207-316.

Burridge, R. (1969) Spherically symmetric differencial equations, the rotation group, and tensor spherical functions. Proc. Camb. Phil. Soc. 65 157.

Phinney, R.A. and Burridge, P. (1973) Representation of the elastic-gravitational excitation of a spherical Earth model by generalized spherical harmonics. Geophys. J. R. astr. Soc. 34 451-487.